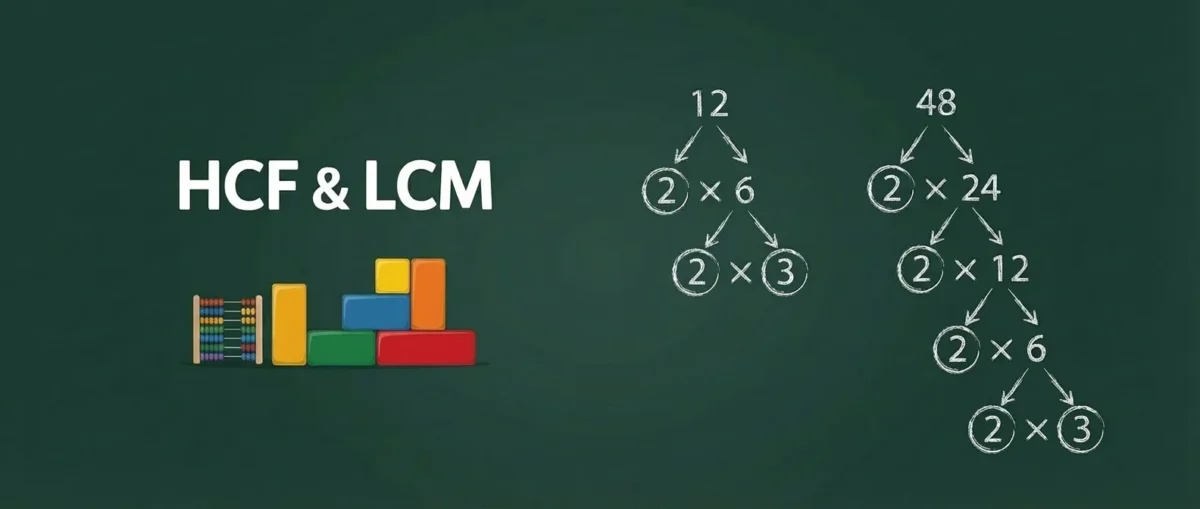
HCF and LCM
Learn to find Highest Common Factor and Lowest Common Multiple with step-by-step explanations
🎯 What You’ll Learn Today
- What HCF and LCM mean in simple terms
- Easy methods to find HCF and LCM
- Prime factorization method for larger numbers
- How to use them in everyday problems
🔢 What is HCF (Highest Common Factor)?
💡 Simple Definition
The HCF is the biggest number that divides evenly into two or more numbers.
Easy Example:
Let’s find the HCF of 12 and 18:
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
- Common factors: 1, 2, 3, 6
- HCF = 6 (the biggest one that’s the same)
📝 Simple Method to Find HCF:
- List all factors of each number
- Find the factors that are the same in both lists
- Pick the biggest one – that’s your HCF!
🔢 Prime Factorization Method for HCF
This is a more advanced method that’s very useful for larger numbers:
Step 1: Find Prime Factors
Break each number down into its prime factors (numbers that can only be divided by 1 and themselves).
💡 Example: Prime factors of 12 and 18
12 = 2 × 2 × 3 = 2² × 3
18 = 2 × 3 × 3 = 2 × 3²
Step 2: Find HCF using Prime Factors
For HCF: Multiply the common prime factors using the LOWEST powers
- Common prime factors: 2 and 3
- Lowest power of 2: 2¹ (appears as 2² in 12, but 2¹ in 18)
- Lowest power of 3: 3¹ (appears as 3¹ in 12, but 3² in 18)
- HCF = 2¹ × 3¹ = 2 × 3 = 6
🏠 Real Life Example
Sarah has 12 apples and 18 oranges. She wants to make gift bags with the same number of apples and oranges in each bag, using all the fruit. What’s the most bags she can make?
Answer: She can make 6 bags (the HCF of 12 and 18), with 2 apples and 3 oranges in each bag.
🔄 What is LCM (Lowest Common Multiple)?
💡 Simple Definition
The LCM is the smallest number that both numbers divide into evenly.
Easy Example:
Let’s find the LCM of 4 and 6:
- Multiples of 4: 4, 8, 12, 16, 20, 24…
- Multiples of 6: 6, 12, 18, 24, 30…
- Common multiples: 12, 24, 36…
- LCM = 12 (the smallest one that’s the same)
📝 Simple Method to Find LCM:
- List the first several multiples of each number
- Find the multiples that are the same in both lists
- Pick the smallest one – that’s your LCM!
🔢 Prime Factorization Method for LCM
Find LCM using Prime Factors
For LCM: Multiply all prime factors using the HIGHEST powers
Using our example: 12 = 2² × 3¹ and 18 = 2¹ × 3²
- All prime factors: 2 and 3
- Highest power of 2: 2² (from 12)
- Highest power of 3: 3² (from 18)
- LCM = 2² × 3² = 4 × 9 = 36
🎯 Memory Tip:
- HCF = Use Lowest powers
- LCM = Use Highest powers
📝 Another Example: 24 and 36
Step 1: Find prime factors
- 24 = 2 × 2 × 2 × 3 = 2³ × 3¹
- 36 = 2 × 2 × 3 × 3 = 2² × 3²
Step 2: Find HCF (lowest powers)
- HCF = 2² × 3¹ = 4 × 3 = 12
Step 3: Find LCM (highest powers)
- LCM = 2³ × 3² = 8 × 9 = 72
Check: HCF × LCM = 12 × 72 = 864, and 24 × 36 = 864 ✓
🏠 Real Life Example
Tom’s bus comes every 4 minutes. Jane’s bus comes every 6 minutes. If both buses just arrived, how long until they arrive together again?
Answer: In 12 minutes (the LCM of 4 and 6), both buses will arrive at the same time.
⚡ The Magic Connection
Useful Trick for Checking
HCF × LCM = First Number × Second Number
Example with 12 and 18:
HCF = 6, LCM = 36
Check: 6 × 36 = 216 and 12 × 18 = 216 ✓
✅ Quick Check Method
Before you finish any question:
- ✓ Does your HCF divide into both original numbers?
- ✓ Do both original numbers divide into your LCM?
- ✓ Does HCF × LCM = number₁ × number₂?
🎯 Remember These Key Points:
- HCF is always smaller than or equal to the smallest original number
- LCM is always bigger than or equal to the largest original number
- Show your working – even if you know the answer
- Check your answers using the magic connection
- Read word problems carefully – are they asking for HCF or LCM?
Practice Problems
Test your understanding with these problems. Use the prime factorization method and show your working.
1. Find the HCF and LCM of 24 and 36.
View Answer
Step 1: Prime Factorization
$$24 = 8 [[times]] 3 = 2^3 [[times]] 3^1$$
$$36 = 4 [[times]] 9 = 2^2 [[times]] 3^2$$
Step 2: Find the HCF (lowest powers of common factors)
Common factors are 2 and 3. Lowest power of 2 is $2^2$. Lowest power of 3 is $3^1$.
$$[[text{HCF}]] = 2^2 [[times]] 3^1 = 4 [[times]] 3 = 12$$
Step 3: Find the LCM (highest powers of all factors)
All factors are 2 and 3. Highest power of 2 is $2^3$. Highest power of 3 is $3^2$.
$$[[text{LCM}]] = 2^3 [[times]] 3^2 = 8 [[times]] 9 = 72$$
Answer: HCF = 12, LCM = 72
2. Find the HCF and LCM of 50 and 120.
View Answer
Step 1: Prime Factorization
$$50 = 2 [[times]] 25 = 2^1 [[times]] 5^2$$
$$120 = 12 [[times]] 10 = (4 [[times]] 3) [[times]] (2 [[times]] 5) = (2^2 [[times]] 3) [[times]] (2 [[times]] 5) = 2^3 [[times]] 3^1 [[times]] 5^1$$
Step 2: Find the HCF (lowest powers of common factors)
Common factors are 2 and 5. Lowest power of 2 is $2^1$. Lowest power of 5 is $5^1$.
$$[[text{HCF}]] = 2^1 [[times]] 5^1 = 2 [[times]] 5 = 10$$
Step 3: Find the LCM (highest powers of all factors)
All factors are 2, 3, and 5. Highest power of 2 is $2^3$. Highest power of 3 is $3^1$. Highest power of 5 is $5^2$.
$$[[text{LCM}]] = 2^3 [[times]] 3^1 [[times]] 5^2 = 8 [[times]] 3 [[times]] 25 = 24 [[times]] 25 = 600$$
Answer: HCF = 10, LCM = 600
3. Two lighthouses flash their lights every 20 seconds and 30 seconds respectively. If they flash together at 7:00 PM, when will they next flash together?
View Answer
This is an LCM problem because we are looking for the next time an event will happen together (a common multiple of the times).
We need to find the LCM of 20 and 30.
Step 1: Prime Factorization
$$20 = 4 [[times]] 5 = 2^2 [[times]] 5^1$$
$$30 = 3 [[times]] 10 = 2^1 [[times]] 3^1 [[times]] 5^1$$
Step 2: Find the LCM (highest powers of all factors)
All factors are 2, 3, and 5. Highest power of 2 is $2^2$. Highest power of 3 is $3^1$. Highest power of 5 is $5^1$.
$$[[text{LCM}]] = 2^2 [[times]] 3^1 [[times]] 5^1 = 4 [[times]] 3 [[times]] 5 = 60$$
The LCM is 60. This means they will flash together every 60 seconds, or 1 minute.
Answer: They will next flash together at 7:01 PM.
Interactive Quiz
Check your knowledge with this quick quiz!
1. Which term describes the largest number that divides exactly into two or more numbers?
2. What is the HCF of 18 and 30?
3. What is the LCM of 12 and 28?
4. To find the LCM using prime factorization, you multiply all the prime factors using their...
5. A baker has two long cakes. One is 30 cm long and the other is 50 cm long. She wants to cut them into equal-sized pieces without any waste. What is the LCM of the lengths?
HCF & LCM Calculator
Enter Numbers
Auto-calculation: Results update automatically as you type!
